Most traditional grid-based board games are played in Euclidean space. This is straightforward and easy to understand but topologically boring.
Why not spruce up the classic grid-based game of chess by modifying it to be played on a non-Euclidean board?
The simplest way to transform a standard board into a non-Euclidean board is to connect the sides of the board together. Connecting the squares on adjacent sides to each other creates a board with an inherently spherical topology. In contrast, connecting the squares on opposite sides can lead to a board with a toroidal structure. A twist in the way the squares are connected can lead to a board with the topology of a klein bottle.
Connecting opposite sides of a chess board (in the diagram above, red sides connect to blue sides) leads to a board with a toroidal structure.
While these macro structures are interesting, they are not clearly well suited for chess. In particular, none of these boards have edges. Thus, it is impossible for a Pawn to reach the edge of the board and become a Queen. Actually, for all we know chess has always been played on boards with these macrostructures, and we just “walled off” a section that was locally equivalent to a subsection of a Euclidean space.
How can we create a non-Euclidean board that does not lose the edge constraints of the original Chess board? One way is to connect random squares to each other by the edges. We will refer to these kinds of connections as “chutes” in homage to a classic board game with these kinds of connections – Chutes and Ladders. Chutes will be shown as blue lines in the diagrams below.
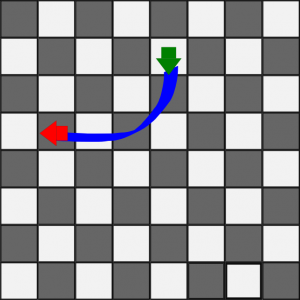
The side of the tile going into the “top” of a chute connects to the side of the tile coming out of the “bottom” of that chute.
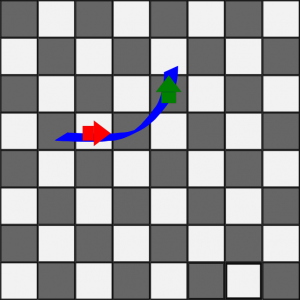
For example, the green “pawn”, above, moves forward one square to the red position. Notice that the pawn is now moving sideways, and can be Queen-ed on its next move. This variant of non-Euclidean chess is best played with pieces with some obvious indication of directionality on them, so that you don’t lose track of their traveling directions.
In order for the board to be connected, we map the tiles that come out of the tops and bottoms of each chute and ladder to each other.
The green piece above ends up where the red piece is when it moves forward one space.
At this point, it is pretty clear how to travel across the sides of the tiles, but what it means to travel diagonally, like a bishop, is less well defined. We will use a “slide-left” metric* to define diagonal moves.
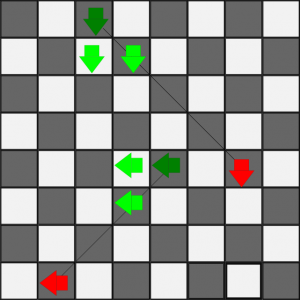
Consider any diagonal move. It can be represented as moving forward one space in one of the four cardinal directions and then sliding to the left one space repeatedly until the destination is reached.
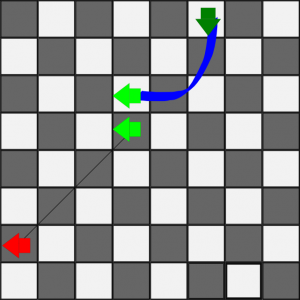
By describing each diagonal move as a series of horizontal and vertical moves, the diagonal movement of pieces through chutes becomes clear.
In the figure above, the green piece begins a diagonal move by moving 1 forward through a chute, then sliding left. The diagonal move can continue until it hits the edge of the board and can no longer complete a “forward one, left one” series.
Note that knights still get to choose whether they move over two and up one or vice versa, and so may easily have more valid destinations than normal.
It is notable that this sort of non-Euclidean chess board is rather unlikely to be fair if you use randomly chosen chutes (perhaps an advantage if you want to handicap players of uneven ability). Can you design a chess board with a single chute such that White as a mate in one?
There are many other fascinating games that you can try playing along similar lines. In one variant of this game, players take turns moving, then adding a new chute to the board. The second post in this series will explore playing chess on a hyperbolic checkerboard (an idea first mentioned to me by Roice Nelson). Are there any other interesting boards that you can imagine playing chess on?
* As David Dalrymple and other people with a better ability to not confuse terminology than me might note: “slide-left” is not a “metric”. It is a homomorphism from the free group on {(1,0),(1,1),(0,1),(-1,1)} to the free group on {(1,0),(0,1)} which preserves actions on the square lattice.