April 2014 – Andrea Hawksley

My gift for Gathering For Gardner 11 was a set of pre-cut playing cards that can be used to assemble a cute geometric construction. The final construction looks like this:

It’s a fun design where the interior figure is clearly a dodecahedron, but, since each card represents two faces of the dodecahedron, the symmetry group represented is pyritohedral.

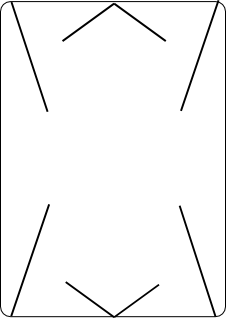
Here is a template that you can print out and cut up to make your own set of cards for this construction.

Your slotted cards should look like this:

You will need six of them to create your ball. Each card should be folded in half “hamburger-style”.

You can join two cards, slotting the two short cuts on one side of one card into two adjacent long cuts on another. All the cards slot into all of the other cards in this same way.

Adding a third card starts to get tricky. The three cards slot together to form a three way join. This is pretty difficult to explain, but here are a bunch of pictures. Don’t worry! Once you have one three-way corner done, the rest are put together the same. By the time you finish, you’ll be a pro!

Now is a great time to take a peek at the inside of your ball before you start closing it up. Can you see the dodecahedron forming?

The rest of this model pretty much follows from the steps previously described. Keep adding pieces like above until your ball is complete! Here are some pictures of the finished ball from different angles.

Today marks the beginning of Mathematics Awareness Month, and this year’s theme is Martin Gardner. Coincidentally, I recently returned from my second trip to the Gathering 4 Gardner (G4G), a recreational math conference with a focus on the sorts of things that Martin Gardner wrote about in is Scientific American column, such as puzzles, magic, mathematical art and other recreational mathematics.

Pretty much everyone who attends is really neat and has done something really cool that was directly or indirectly inspired by Martin Gardner. A number of the attendees are actually professional magicians and one highlight of the event is the astounding evening events and shows.

In addition to organized talks, the highlight of the conference is often just talking to people. I know quite a lot about polyhedra, but I had an interesting discussion with John Conway (who also had the honor of being the theme for this year’s conference) about the naming of the rhombicuboctahedron where I learned some new things that I hadn’t known previously.

My favorite part of G4G is an afternoon excursion devoted to talking and learning things from other attendees, and also to large art sculpture “barn-raisings”. I was one of the six artists that participated in the sculpture event and organized a group to make a construction out of hair bands, a fun precursor to my later talk on a hair tie 120-cell (a 120-cell is a regular 4-dimensional polychoron made out of 120 dodecahedral cells). My creation used a technique for making large geometric constructions out of hair ties that I learned from Zachary Abel at the last G4G.

Here’s a picture of some the team that helped me construct the hair tie construction. Thanks to everyone that helped!

The hair band construction consists of a tetrahedron of green hair bands inside a cube of purple bands, inside an octahedron of black bands. You can see the tetrahedron in the cube fairly well in this close up shot.

G4G has a formal puzzle and art exchange as well as many informal ones. Here are a few of the neat things that I got from G4G11. If you were in doubt about my claim that the people that attend G4G are collectively really cool and amazing, these pictures should probably lay your doubts to rest.

George Hart’s gift exchange item was a set of pre-cut cards that assemble into a Tunnel Cube.

Edmund Harriss laser cut sets of paper pieces that cleverly slotted together. I took two chiral sets of five-pronged pieces and combined them to make this neat woven ball.

Eve Torrence gave me a set of pieces for her gorgeous “Small Ball of Fire”. I love the choice of foam as the material, as it is very forgiving and easy to assemble.

I got this surprisingly fun and meditative marble labyrinth from Bob Bosch.

And two different versions of a square to equilateral triangle dissection. The hinged one was 3d printed by Laura Taalman. The wooden piece is from Dick Esterle

Finally, the gift exchange includes many fun puzzles and papers that are interesting, but not as photogenic. I particularly liked the “turn MI into MU” (solvable variant) puzzle from Henry Strickland.

In my next post, I will talk about my own G4G exchange gift, that you can construct at home even if you didn’t attend G4G!

Month: April 2014

Six Card Ball

Gathering for Gardner 11