How would one make mathematical cuisine? Not just food that looks mathematical (like math cookies), but something that you truly have to eat and taste in order to experience its mathematical nature.
Henry Segerman proposed this question, and today we had our first experience tasting the answer. A masterpiece of mathematical art, the answer I came up with is simple enough that anyone can make it at home, surprisingly visually beautiful, delicious…
Layered Drinks!
Not just any layered drinks, of course. In our layered lemonade, the intensity of flavors as you go down the layers increases exponentially. The sugar and lemon juice proportions for the same quantity of liquid increase according to the Fibonacci sequence. The sweeter layers are denser and naturally keep separated lower down. Indeed, the nature of layered drinks is that they are monotonically increasing in sweetness (and/or decreasing in alcohol). Thus, there is an intrinsic mathematical property to all layered drinks.
Additionally, the ratio of sugar to lemon juice in our lemonade isn’t constant. The top layer of our drink is 1 part lemon, while the second layer is 1 part sugar syrup. Following the Fibonacci rule, each subsequent layer has proportions that are the sum of the previous two layers proportions.
Layer 3 is 1 part lemon, 1 part sugar. Layer 4 is 1 part lemon, 2 parts sugar, and so on.
Generically, for layer n > 2, there are fib(n-1) parts sugar and fib(n-2) parts lemon juice. These are adjacent Fibonacci numbers, so as the drink is consumed the ratio of lemon to sugar approximates the Golden Ratio. This drink may be the worlds first tastable example of the relationship between the Fibonacci sequence and the golden ratio!
Surprisingly, using golden ratio relative proportions of lemon juice and simple syrup actually seems to make rather good lemonade. When consumed, the beverage starts out fairly flavorless, then rapidly ramps up. It also alternates between being a bit sweet to being slightly sour (of course this is a matter of personal taste), as the approximation of the golden ratio alternates between being slightly high and slightly low.
You too can make Fibonacci lemonade and experience the taste of exponential flavor, the golden ratio, and the Fibonacci sequence. Just follow the recipe below!
Ingredients and Materials:
Lemon Juice
SImple Syrup (1 cup sugar dissolved in 1 cup water)
Water
Food Coloring (optional but makes it pretty)
Ice or a spoon for slow pouring (the ice free strategy is much harder)
The Method
You must start with the sweetest and densest layer and work your way backwards up the drink. I describe the layers for a 7 layer drink below, although you may choose to make a different number of layers to start. The drink could also be made without the first layer, in which case it is neatly just two offset increasing Fibonacci sequences, one per ingredient.
First, fill your glasses with ice. Then, do the following steps for each layer. Finally, sip your mathematical masterpiece.
- Add the proportions of lemon juice and simple syrup indicated below to your liquid measuring cup.
- Add food coloring if desired.
- Fill measuring cup to the 4 oz. (1/2 cup) line.
- Stir to blend all ingredients in your measuring cup.
- Slowly pour a layer from your measuring cup into your drink glasses. You want to pour directly onto an ice cube, the ice cubes are there to slow down your liquid as it goes down the cup and to help keep the layers distinct. (You can pour the first layer normally)
The Layers
- 1 tsp. lemon juice
- 1 tsp. simple syrup
- 1 tsp. lemon juice, 1 tsp. simple syrup
- 1 tsp. lemon juice, 2 tsp. simple syrup
- 2 tsp. lemon juice, 3 tsp. simple syrup
- 3 tsp. lemon juice, 5 tsp. simple syrup
- 5 tsp. lemon juice, 8 tsp. simple syrup
Tips
- Many simple syrups are 2 parts sugar to 1 part water. If yours is like this, halve the amount of sugar you are using (or it will probably be far too sweet).
- For a more authentic, less watered down experience, you need to make your drinks without ice. This is much harder, and I don’t actually recommend it unless you are patient or really know what you are doing. You can find directions for layering without ice here.
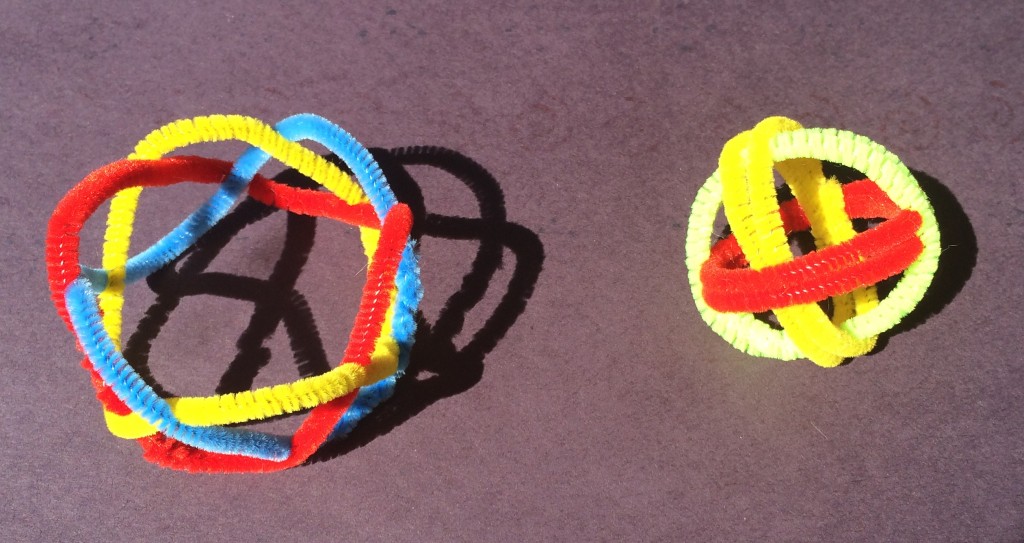Colorful pipecleaners also let you create pretty geometric star sculptures. This 4-axis star is a make-at-home version of the stars developed by John Kostick and, independently, Akio Huzime. This star has 8 points and octahedral symmetry. As you can see from John and Akio’s websites, many other stars based on other symmetries are possible. If you too have a plethora of pipe cleaners, you might consider trying to create some of them yourself.
Squawk! It’s a Polly-hedron.