Posted on

Introducing the Tip Palindromator

It’s surprising to me how many people I know have independently taken to tipping such that the total is palindromic. The reasons for doing so are simple enough:

  1. It’s entertaining (for you and for the staff processing your charge)
  2. It helps you quickly verify credit card charges and check for potential fraudulence
  3. After a delicious sleepy meal late at night, one definitely needs to practice one’s mental math abilities…

Ok. We should probably strike #3.

  1. After a delicious sleepy meal late at night, one definitely needs to practice one’s mental math abilities…

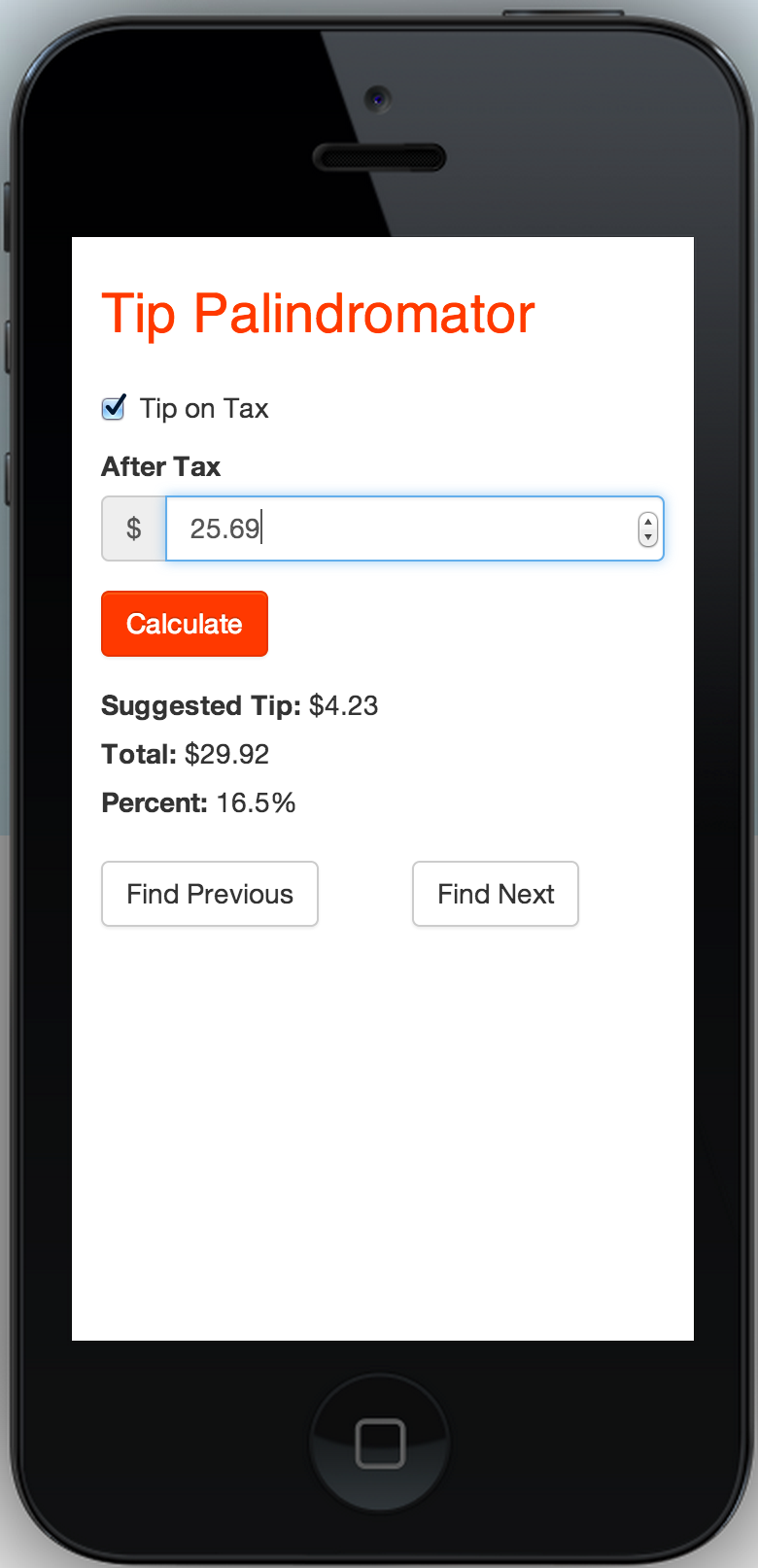
The fact is we’ve all gotten checks where we definitely did not want to have to deal with figuring out precisely how much to tip. After one too many of those, I realized that I needed to create the Tip Palindromator (http://octahedralgroup.org/tip).

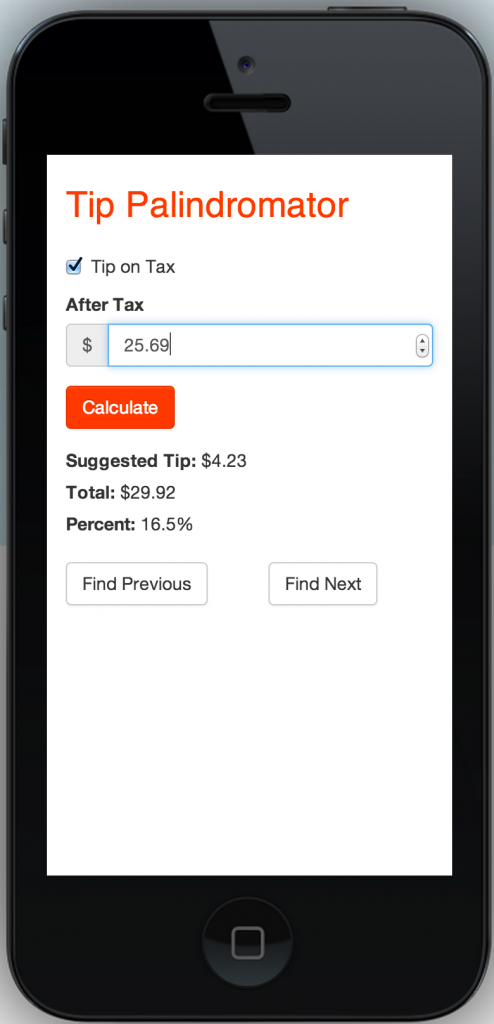
Pasted_Image_5_6_14__2_22_PM

The Tip Palindromator shows up great on mobile web. Want it as an application? Just choose the “add to home screen” option from your Android or iPhone web browser. The “Tip It” application is a great addition to the home screen.

It lets you quickly input your total bill and automatically finds a potential palindromic tip*, which can be adjusted up and down to find the perfect tip percentage.

Now, even the half-asleep can leave palindromic tips with ease.

* Note: I use this term to refer to a tip that leaves a total that is a palindrome, rather than a tip that is itself a palindrome.
Posted on

Six Card Ball

My gift for Gathering For Gardner 11 was a set of pre-cut playing cards that can be used to assemble a cute geometric construction. The final construction looks like this:

6 Card Ball

It’s a fun design where the interior figure is clearly a dodecahedron, but, since each card represents two faces of the dodecahedron, the symmetry group represented is pyritohedral.

Here is a template that you can print out and cut up to make your own set of cards for this construction.

6-card-ball-template

Your slotted cards should look like this:

Vnumx

You will need six of them to create your ball. Each card should be folded in half “hamburger-style”.

VHn65

You can join two cards, slotting the two short cuts on one side of one card into two adjacent long cuts on another. All the cards slot into all of the other cards in this same way.

ZjrBj 9RFUy

Adding a third card starts to get tricky. The three cards slot together to form a three way join. This is pretty difficult to explain, but here are a bunch of pictures. Don’t worry! Once you have one three-way corner done, the rest are put together the same. By the time you finish, you’ll be a pro!

 

Now is a great time to take a peek at the inside of your ball before you start closing it up. Can you see the dodecahedron forming?

mWZA0

The rest of this model pretty much follows from the steps previously described. Keep adding pieces like above until your ball is complete! Here are some pictures of the finished ball from different angles.

 

 

 

 

Posted on

Gathering for Gardner 11

Today marks the beginning of Mathematics Awareness Month, and this year’s theme is Martin Gardner. Coincidentally, I recently returned from my second trip to the Gathering 4 Gardner (G4G), a recreational math conference with a focus on the sorts of things that Martin Gardner wrote about in is Scientific American column, such as puzzles, magic, mathematical art and other recreational mathematics.
Pretty much everyone who attends is really neat and has done something really cool that was directly or indirectly inspired by Martin Gardner. A number of the attendees are actually professional magicians and one highlight of the event is the astounding evening events and shows.
In addition to organized talks, the highlight of the conference is often just talking to people. I know quite a lot about polyhedra, but I had an interesting discussion with John Conway (who also had the honor of being the theme for this year’s conference) about the naming of the rhombicuboctahedron where I learned some new things that I hadn’t known previously.
My favorite part of G4G is an afternoon excursion devoted to talking and learning things from other attendees, and also to large art sculpture “barn-raisings”. I was one of the six artists that participated in the sculpture event and organized a group to make a construction out of hair bands, a fun precursor to my later talk on a hair tie 120-cell (a 120-cell is a regular 4-dimensional polychoron made out of 120 dodecahedral cells). My creation used a technique for making large geometric constructions out of hair ties that I learned from Zachary Abel at the last G4G.
Here’s a picture of some the team that helped me construct the hair tie construction. Thanks to everyone that helped!
DSC_9392
The hair band construction consists of a tetrahedron of green hair bands inside a cube of purple bands, inside an octahedron of black bands. You can see the tetrahedron in the cube fairly well in this close up shot.
DSC_9386

G4G has a formal puzzle and art exchange as well as many informal ones. Here are a few of the neat things that I got from G4G11. If you were in doubt about my claim that the people that attend G4G are collectively really cool and amazing, these pictures should probably lay your doubts to rest.

George Hart’s gift exchange item was a set of pre-cut cards that assemble into a Tunnel Cube.DSC_9420
Edmund Harriss laser cut sets of paper pieces that cleverly slotted together. I took two chiral sets of five-pronged pieces and combined them to make this neat woven ball.
DSC_9422
Eve Torrence gave me a set of pieces for her gorgeous “Small Ball of Fire”. I love the choice of foam as the material, as it is very forgiving and easy to assemble.
DSC_9424

I got this surprisingly fun and meditative marble labyrinth from Bob Bosch.

DSC_9423
And two different versions of a square to equilateral triangle dissection. The hinged one was 3d printed by Laura Taalman. The wooden piece is from Dick Esterle
DSC_9427

Finally, the gift exchange includes many fun puzzles and papers that are interesting, but not as photogenic. I particularly liked the “turn MI into MU” (solvable variant) puzzle from Henry Strickland.

In my next post, I will talk about my own G4G exchange gift, that you can construct at home even if you didn’t attend G4G!
Posted on

Why can’t Pi and Tau be friends?

π day used to be a straightforward holiday for people who love mathematics. Who could possibly dislike a holiday to celebrate a number that has been celebrated across cultures and throughout history? The Egyptians and Babylonians approximated the ratio of the circumference of a circle to its diameter. The same in Ancient India, China, and Greece. The symbol π itself is newer, but is still over 300 years old.

Only recently have Tauists come along and started their arguments that Pi is wrong. Since then, the Pi and Tau adherents seem to have turned our circles into boxing rings, with Pi on one side and Tau in the other.

The Tauists start it off with a series of quick jabs.  Tau is fundamentally simpler. Radius is more fundamental than diameter, the fundamental constant should be based on radius. Radians finally make sense, it goes against intuition to have 2 Pi radians in a circle. Pi is off by a factor of 2. It is unnatural and confusing. It is wrong!

The Pious punch back that Pi has been the constant for thousands of years, that it’s what everyone knows, that nobody naturally draws a line going halfway across a circle. Tauists demonstrate selective bias to prove their point. The area of 1/4 of a unit circle is Pi/4, or Tau/8. Tau is off by a factor of 2. It is unnatural and confusing. It is wrong!

But, in the midst of all this bickering, we lose the fundamental reason why Pi and Tau are so cool. When we get held up in the details, we forget how magical it is that the ratio of a diameter or radius of a circle to its circumference is somehow not something that can be expressed as a ratio at all. That somehow the observed perfection of a circle is due to something truly transcendental. That a circle is itself the perfect shape, minimizing surface area to volume, exhibiting the same curvature everywhere around itself until you get back to exactly where you started.

Tau and Pi aren’t that different. They’re both irrational, they’re both transcendental, they solve all of the same problems. They are, in fact, the same number give or take a factor of 2. Maybe we can just teach everyone both and let people choose for themselves whichever one is easiest for them?

If we celebrate both, that’s twice as many days to get people excited about mathematics. It’s twice as many days to eat pie and appreciate how round it is.

I mean, Tau is just 2*Pi. Er, Pi is just Tau/2. Fine. Tau and Pi differ by just a factor of 2. Sorry. Pi and Tau differ by just a factor of 2. Really, why are we arguing?

So this π day, lets agree to shake hands, stop fighting, and eat some Tau-co Pi. It’s delicious and the fundamental constant that we know and love makes just as beautiful circles whether it’s 3.14… or 6.28…

Thanks guys. Happy Pi day!