Math Art – Page 3 – Andrea Hawksley

April 17, 2014June 12, 2014

Six Card Ball

My gift for Gathering For Gardner 11 was a set of pre-cut playing cards that can be used to assemble a cute geometric construction. The final construction looks like this:

It’s a fun design where the interior figure is clearly a dodecahedron, but, since each card represents two faces of the dodecahedron, the symmetry group represented is pyritohedral.

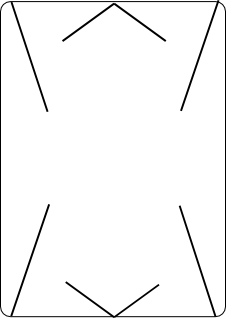
Here is a template that you can print out and cut up to make your own set of cards for this construction.

Your slotted cards should look like this:

You will need six of them to create your ball. Each card should be folded in half “hamburger-style”.

You can join two cards, slotting the two short cuts on one side of one card into two adjacent long cuts on another. All the cards slot into all of the other cards in this same way.

Adding a third card starts to get tricky. The three cards slot together to form a three way join. This is pretty difficult to explain, but here are a bunch of pictures. Don’t worry! Once you have one three-way corner done, the rest are put together the same. By the time you finish, you’ll be a pro!

Now is a great time to take a peek at the inside of your ball before you start closing it up. Can you see the dodecahedron forming?

The rest of this model pretty much follows from the steps previously described. Keep adding pieces like above until your ball is complete! Here are some pictures of the finished ball from different angles.

April 1, 2014October 4, 2014

Gathering for Gardner 11

Today marks the beginning of Mathematics Awareness Month, and this year’s theme is Martin Gardner. Coincidentally, I recently returned from my second trip to the Gathering 4 Gardner (G4G), a recreational math conference with a focus on the sorts of things that Martin Gardner wrote about in is Scientific American column, such as puzzles, magic, mathematical art and other recreational mathematics.

Pretty much everyone who attends is really neat and has done something really cool that was directly or indirectly inspired by Martin Gardner. A number of the attendees are actually professional magicians and one highlight of the event is the astounding evening events and shows.

In addition to organized talks, the highlight of the conference is often just talking to people. I know quite a lot about polyhedra, but I had an interesting discussion with John Conway (who also had the honor of being the theme for this year’s conference) about the naming of the rhombicuboctahedron where I learned some new things that I hadn’t known previously.

My favorite part of G4G is an afternoon excursion devoted to talking and learning things from other attendees, and also to large art sculpture “barn-raisings”. I was one of the six artists that participated in the sculpture event and organized a group to make a construction out of hair bands, a fun precursor to my later talk on a hair tie 120-cell (a 120-cell is a regular 4-dimensional polychoron made out of 120 dodecahedral cells). My creation used a technique for making large geometric constructions out of hair ties that I learned from Zachary Abel at the last G4G.

Here’s a picture of some the team that helped me construct the hair tie construction. Thanks to everyone that helped!

The hair band construction consists of a tetrahedron of green hair bands inside a cube of purple bands, inside an octahedron of black bands. You can see the tetrahedron in the cube fairly well in this close up shot.

G4G has a formal puzzle and art exchange as well as many informal ones. Here are a few of the neat things that I got from G4G11. If you were in doubt about my claim that the people that attend G4G are collectively really cool and amazing, these pictures should probably lay your doubts to rest.

George Hart’s gift exchange item was a set of pre-cut cards that assemble into a Tunnel Cube.

Edmund Harriss laser cut sets of paper pieces that cleverly slotted together. I took two chiral sets of five-pronged pieces and combined them to make this neat woven ball.

Eve Torrence gave me a set of pieces for her gorgeous “Small Ball of Fire”. I love the choice of foam as the material, as it is very forgiving and easy to assemble.

I got this surprisingly fun and meditative marble labyrinth from Bob Bosch.

And two different versions of a square to equilateral triangle dissection. The hinged one was 3d printed by Laura Taalman. The wooden piece is from Dick Esterle

Finally, the gift exchange includes many fun puzzles and papers that are interesting, but not as photogenic. I particularly liked the “turn MI into MU” (solvable variant) puzzle from Henry Strickland.

In my next post, I will talk about my own G4G exchange gift, that you can construct at home even if you didn’t attend G4G!

March 3, 2014June 12, 2014

Cookie Shapes

Vi made a video about the our cookie making adventures, in which she proves that I have some pretty amazing friends. Enjoy!

Update: She also made this blog post about her process.

Gwen’s blog post about our cookie making is here.

February 14, 2014June 12, 2014

3Doodling with my 3Doodler

Like tens of thousands of other people imagining epic 3-dimensional doodling abilities, I purchased a 3Doodler on Kickstarter. Last weekend, I decided to sit down and actually try doodling something cool.

The first problem that I discovered when 3Doodling is that it really isn’t very easy to doodle accurately in the air. The plastic takes just enough time to dry that you still have to deal with sag. On the other hand, the plastic does detach easily from paper. People seem to mostly suggest tracing 2-D templates and then putting the pieces together.

My 3Doodled piece was made out of 20 interwoven 3-pronged pieces that were doodled onto a flat 2D template that I sketched out quickly beforehand. It is based off of the Medial Triambic Icosahedron. The red outline in my template below is representative of the full face of the medial triambic icosahedron. The blue line is the template I traced. This is a portion of the face selected such that the faces would spiral around each other rather than intersect in my final model.

The second problem that is that (at least on my device) the feed mechanism is flaky and plastic comes out in spurts followed by nothing, which makes drawing accurately even on paper rather difficult. This problem makes drawing in air seem pretty impossible. My device also has a relatively minor issue of the top “fast” button having a tendency to catch and get stuck in the “on” position.

You can see the resultant unevenness in this close-up of one vertex where some of the lines are notably thinner or blobbier than others.

The last issue is that the 3Doodler is an ergonomic nightmare. Holding the 3Doddler for several hours while pressing the “extrude” button with my thumb gave me sufficiently severe thumb and wrist pain that I am unlikely to do much 3Doodling in the future.

All of this is unfortunate because despite it’s issues, the 3Doodler is really quite nifty and fun to play with. If I was able to use it without wrist pain, I would be seriously considering how to purchase more plastic (as you can see, I actually ran out of red towards the end of my model and started connecting corners with black). There is definitely something rewarding about drawing something very solid and physical, and as far as end results go, I was actually reasonably pleased with my doodle.

As I’ve mentioned before, a lot of models like this one cast impressive shadows. Here are some pictures of this model’s shadow.

February 3, 2014June 12, 2014

Shortbraid and other geometric cookies

What happens when you combine three recreational math artists with a fantastic pastry chef?

Last weekend, Vi Hart, Gwen Fisher, Ruth Fisher and I got together to try this experiment. Ruth provided several colors of shortbread dough and white chocolate “glue” and a few assorted cookie cutters. Gwen took photos (shown with permission below) and Vi took a bunch of video.

Our first idea was to make polyhedra cookies. The hexagon cookie cutter seemed to suggest truncated tetrahedra, octahedra, and icosahedra. We tried making one of each.

Assembly was a bit tricky and required the use of an assortment of cardboard jigs to keep pieces in place while the chocolate dried.

While our hexagon cookies were baking, Vi got started making a rhombic dodecahedron. We used a straight-edge to cut rhombi with the correct dimensions.

She wanted to have little cut-out holes in her polyhedron, and used a rhombic cookie cutter that happened to have just the correct dimensions to tile the plane nicely.

Which, of course, got us thinking about more interesting geometric tilings. For example, non-periodic Penrose tilings. Everyone likes the kite dart tiling and we made ourselves some cookie cutters out of card stock to generate kites and darts quickly.

A real math cookie party isn’t complete with out some fractals (here we have some Sierpinski Tetrahedra)…

and some shortbread “shortbraids”. The three rings here form an 18-crossing Brunnian link.